まだ最小二乗法で消耗してるの？ ～Passing Bablok法について～

【イントロ】
与えられたデータの傾向を見る、つまり回帰分析の一つとして、直線でフィッティングする方法が挙げられます。
ココで問題となるのが、「どうやって直線の傾き(と切片)を求めるか」という点です。
代表的な方法が最小二乗法です。目的の直線を
$y=ax$
と仮定します。データ点$y$と求めたい直線との差の二乗を誤差として、すべての点に対する誤差の和を最小化する傾き$a$を求める方法です。
具体的には誤差の和を
$E=\sum_{i=1}^{n}(y_i－ax_i)^2$
とすると、$a$について最小値が欲しいので、
$\frac{\partial E}{\partial a}=0$
となる$a$を求めれば良いです。整理すると、
$a=\frac{\sum_{i=1}^{n}(x_i－x_{average})(y_i－y_{average})}{\sum_{i=1}^{n}(x-x_{average})^2}$
となります。
　最小二乗法は直観的にもちょうどよい直線を見つけてくれそうで、最強の方法に見えます。しかし、いくつかの課題があります。まず一つが、外れ値に弱いという点です。えっちですね。つまり、ノイズ等の影響でデータ点の集合から大きくハズレた点が存在すると、その点に引きずられて傾き$a$が大きく変化してしまうという点です。
　また、別の問題として、最小二乗法は暗にデータが正規分布に従った誤差を持つことを仮定している点が挙げられます。今回最小化すべき誤差をデータ点と直線の差の二乗和として与えましたが、これはデータ点の周りに分散一定の誤差が正規分布している場合に導かれる最尤推定解と対応しています。詳細はPRMLを参照。
さて、それではこうした最小二乗法の呪縛から解き放たれた、 回帰モデルは存在するでしょうか？そうしたモデルとしては主成分分析等があります
本記事では、そうした手法の中でもノンパラメトリック回帰モデルの一つである”Passing-Bablok法”について、原論文に従った解説とPythonでの実装に取り組みました。
【方法】
Passing-Bablok法はその名の通り、PassingとBablok(PB)により提案された、一次の比例関係を比較するノンパラメトリック回帰モデルです。PBは医療科学分野において2つの実験手法から得られたデータを比較する場面を想定し、現実には誤差の正規分布が成り立たない状況や、外れ値が本質的に含まれてしまう状況が起きうること、すなわち上に述べた最小二乗法の問題点が露呈しうまくいかない状況が生じうることを指摘しています。そこで、最小二乗法に変わる手段として、データ点間の傾きに着目した回帰モデルを提案しています。そこでは、以下の2点の仮定のみを設定します。

1. データ点は連続分布した集合からランダムに取得したもの
2. 比較する2つのデータは同じタイプの誤差分布をもつ(正規分布でなくても良い)。分散は互いに異なってもよいが比例関係にあること。

この比較的弱い仮定のみで、PBは議論を進めています。
次に実際に傾きを求める方法を述べます。微妙に端折っているところがあるので、詳細は原論文を確認ください。

1. n個のデータ点について、すべてのペア$n(n-1)/2$個の傾きを求めます。すなわち
   $S_{ij}=\frac{y_i-y_j}{x_i-x_j} \quad for \quad 1 \leq i<j\leq n$
   として、すべての傾きを計算します。$i=j$の場合は除きます。また、数値の組み合わせによっては傾きの値がゼロや無限大になる可能性もありますが、連続変数を仮定しているので、その確率は実質ゼロと考えます。(そんな奇跡は…起きない…ッ！)
2. つぎに、求めた$S_{ij}$のリストを昇順に並べ変えます。さらに、Kを$S_{ij}<-1$を満たす数として、リストの小さい方からK個除いた新しいリストを作成します。この新リストの中央値が求めたい傾きとなっています。えぇ…。ここで、Kを$S_{ij}<-1$を満たす数として導入したのは、(PB曰く)「傾きが1」という帰無仮説を採用したことに対応しています。

以上です。簡単でしょ？他にも、信頼区間の計算や、線形性の検定といった論点もありますが、ココでは省略します。論文やこちらのページ(PDF)に従えば実装可能です。わたしも理解しきれていません。
このPB法をPythonで実装したプログラムは下記に示しています(大体合ってるはず)。
【結果】
最小二乗法とPB法の比較を下図に示します。まずは外れ値がない場合です。 図の通り、2つの方法がほとんど同じ値を返していることがわかります。

図1、PB法と最小二乗法の比較(外れ値なし)

次に、大きな外れ値を導入した場合を示します。最小二乗法の傾きが、外れ値に引っ張られている一方で、PB法は変わらず正しい値を返しています。この結果から、PB法が外れ値に対してロバストであることがみてとれます。すごいぞPB法！

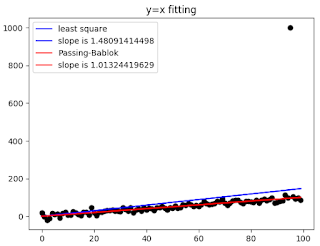図２，PB法と最小二乗法の比較(外れ値あり)

(追記)ちなみに、傾きの分布がどの様になっているか確認するため、ヒストグラム表記したものを図3に示します。ほとんど傾き１の周辺に集まっていることがわかります。

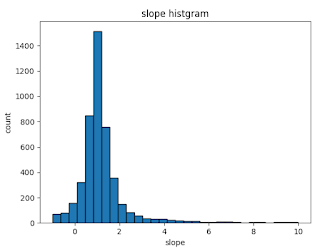図３，傾きの分布(-1から10までを30分割して各区間の個数を表示)

このようにPB法は外れ値への影響が少ない回帰モデルとして、医療科学分野や、メゾスコピック物理の分野で使用されています。
ただ、実際に論文を読んでみていくつか疑問が浮かびます。

1. 原論文では与えられたデータが$y=x$の形にある、つまり傾きが1かどうか調べる手段としてPB法を提案しています。この手法を傾き1以外に拡張してよいのか、よくわかりません。同様の指摘はこちらのページ(PDF)でもなされています。ただし、傾き1以外の場合に対して、おなじアルゴリズムで傾きを計算すると、当然傾きを求めることができます。たすけて。(追記)実際には、データをスケールしてxy軸が1:1になるようにしてから PB法で傾き(と切片)をもとめてもとに戻す、といった手順を踏むらしいです。なるほど、知性がある。
2. 求めたい傾きを、すべての点間の傾きの中央値としていますが、その妥当性がしっくり来ません。助けて。
3. 中央値を求める際、Kだけシフトした中央値を求めていますが、この妥当性もしっくり来ません。タスケテ。

【まとめ】
本記事では、一次の比例関係に対して、最小二乗法とは別のノンパラメトリック回帰モデルであるPassing-Bablok法について説明を試みました。Pythonで実装し、ばらつきをもたせたデータに対して最小二乗法と比較してみると、外れ値に対してロバストな性質を持つことが見て取れました。また、誤差の分布がわからないときにも正当化できるという点も、幅広い分野での使用につながりそうです。ただ、いくつかの疑問点も残ったので、そこを解決できるようにもう少し勉強しないといけないなぁと思いました。
なにか有益な参考書等ありましたら、コメントいただけると幸いです！

タイトル

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

import numpy as np import matplotlib.pyplot as plt import statistics   #グラフの点数 N=100   #x,y座標の作製 x=np.array(range(0, N, 1)) y=np.array(list(1*i + 10*np.random.randn() for i in x))   #外れ値の導入 #y[95]=1000   #Passing-Bablock法 def Passing_Bablok(x,y):     ng_count=0     PB_list=[]       for i in range(N):         for j in range(N):             if i < j:                 slope=(y[i]-y[j])/(x[i]-x[j])                 PB_list.append(slope)                 if slope<-1: :="" a="" a_pb="" a_pb_lower="" a_pb_upper="" c_alpha="(1-0.95/2)*np.sqrt(N*(N-1)*(2*N+5)/18)" color="r" def="" del="" else="" fitting="" label="slope is " least_square="" lower="" ls_coef="" m1="int(round((N_PB_list-C_alpha)/2))" m2="N_PB_list-M1+1" n_pb_list="len(PB_list)" ng_count="" pass="" pb_coef="" pb_list.sort="" pb_list="" pb_lower="PB_list[M1]" pb_upper="PB_list[M2]" plt.legend="" plt.plot="" plt.scatter="" plt.show="" plt.title="" pre="" print="" return="" shift="" str="" sum="" upper="" x-x_ave="" x.max="" x="" x_ave="np.average(x)" y="x" y_ave="np.average(y)"><!---1:-->