愛ある聖しこの夜~AIとの協働によるKK変換の実装~
【イントロ】
今年もクリスマスがやってきました。
Kotoshi・・・Kurisumasu・・・
聖しこの夜ですね。
Kiyoshi・・・Konoyoru・・・
ということで、今回の記事ではKK変換(Kramers–Kronig変換)について、Chat系AIを使って実装に取り組んでみた内容をまとめてみます。
*本記事はあらBさん主催のアドベントカレンダー2024の投稿記事です。
【KK変換とはなにか】
WikiによるとKK変換とは、
「線形応答における周波数応答関数の実部と虚部がヒルベルト変換で関係づけられていることを示した式」
ということになります。
具体的には、複素関数 H(ω)=H_R(ω)+iH_I(ω)を考えます。複素数ωの複素平面の上半面で解析的で、下半面にのみ極をもつとき、極を避けた半円状の積分路を選択すると
∮H(ω')/(ω'-ω)dω'=0
が成り立ちます。
ここで、ω→∞でHが漸近的に0になるとすると、積分路の大円の半径を大きくとることで、
‐iπH(ω)+P∫H(ω)/(ω'-ω)dω'=0
が導かれます。ただし、ここでPは主値積分を表します。
このとき、Hの実部と虚部は独立ではなくなり、以下のような関係式を満たします。
 |
| Wikiより |
この関係式をKramers–Kronigの関係式とよび、この関係式を用いて実部と虚部を変換する処理をKK変換と呼びます。
この関係式を用いることで、周波数応答関数の実部または虚部から、もう一方の値を取得することが可能になります。この結果は、刺激よりも前に結果は生じないという因果律を反映するものとなっています。
*ここの式の導出をちゃんとフォローできてないので、参考文献あればコメント下さい><
この解析手法により、赤外分光法による反射率測定から光学伝導度を求めたり、中性子散乱測定により動的帯磁率の実部と虚部を求めたりすることが可能となります。
今回の記事では、特に反射率から光学伝導度を求める方法について着目しました。
【反射率からどうやって光学伝導度を求めるか】
光学伝導度は物質の電荷応答を表す物理量です。その周波数特性は、伝導電子やフォノンの情報、バンド間遷移の情報、各種相転移に伴うバンド構造の変化や超伝導ギャップなど様々な情報を含んでいます。さらに、高圧下や磁場中でも測定が可能であり、使用する電磁波の波長の侵入長からバルク敏感な測定となっており、最強の測定手段です。
具体的に、反射率R(w)から光学伝導度σ(w)を求める場合を考えてみます。
一般的に、複素誘電率ε’は誘電率の実部εと光学伝導度σを用いて
ε’=N’^2=ε(w)+4πiσ(w)/w
と表されます。wは周波数とします。オメガじゃないのは、ωと変換するのが面倒だからです。ここでN’は複素屈折率
N’=n + ik
とします。
同様に、複素光学伝導度σ’(w)は、
σ’(w)=w(ε’‐ε∞)/4πi
と定義されます。ここでε∞は周波数∞での誘電率です。
唐突ですが、複素反射率r(w)を以下に定義します。
r(w) = R(w)exp(iθ(w))=(N’-1)/(N'+1)
ここでθは光の反射に伴う光の位相の変化です。
両辺の対数を取ると
lnr(w) = lnR(w) +iθ(w)
となります。この式はKKの関係式を満たすため、Rからθを求めることができます。
Rとθが揃えば複素屈折率を介して誘電率εと光学伝導度σも求める事ができます。
すなわち、光学反射率R(w)から光学伝導度σ(w)を求めることが可能になります。
 |
| 逆境無頼カイジ©️より |
実際上は、θ(w)の周波数依存性を求めるためには、周波数ゼロから無限大までのR(w)が必要となるため、測定の工夫や各種近似が必要となります。
例えばw→0では、頑張って低エネルギーまで測定したり、Hagen-Rubensの関係式(R~w^0.5)を用いたりします。w→∞では、放射光測定により高エネルギーの周波数まで反射率を測定してみたり、それでも足りない分はR~w^-4の近似式で外挿します。
つまり、論文などで報告されている反射率から求めた光学伝導度はある種「作られた」データであることに注意が必要であるということになります。
さて、ここからが本題です。今回はこの反射率から光学伝導度を求めるKK変換をPythonで実装することを目指しました。
【Chat系AIを利用したKK変換の実装の取り組み】
今回利用したのは、Anthropic社のAI、Claudeです。課金してOpusモデルを利用しました。使用した理由は、検証時点で数学やコーディングに強いと評判であり、一度Claudeを使ってみたいと思ったためです。また、画像やPDFを読み込んでの応答に対応していることも選んだ理由の1つです。
具体的には、以下のように実行してみました。
- 島津製作所HP「正反射法とクラマース・クローニッヒ解析のイロハ」のKK変換の解説ページを画像化する
- 画像化した説明をClaudeの読み込ませ、内容を解説させる。
- 記載されている内容をPythonコード化するよう指示する
- 出力されたPythonコードをGoogle Colabで実行する。
- エラーが出た場合は、エラー処理をClaudeに問い合わせ解消する
他にも、関連論文をPDFで読み込ませた結果も参考にしました。
以上の様な取り組みを行うことで、1時間程度で結果を可視化することが可能となりました。結果は以下のように比較しました。
- 誘電率のローレンツモデル(物質のバンド間遷移などをモデル化したもの)から直接的に光学伝導度を計算する
- 誘電率のローレンツモデルから反射率を計算し、その反射率をKK変換して光学伝導度と求める
- 1と2の結果を比較する
このようにして得られた結果が以下です。
実際に使用したコードは記事の末尾に記載します。
【考察】
結構簡単にできてしまいました。
所要時間は文献調査からグラフ作成までトータル2時間くらいです。
すごいぞAI!
ただし出てきた結果が正しい結果なのか詳しく調べる必要があります。
例えば、以下の観点が必要です。
- 周波数依存性が既知の結果と対応しているか
- 絶対値が妥当なものとなっているか
- 実際の物質の反射率を入力とした際に正しい結果を返すか
そもそもの処理の改善点として、以下の点があります。
- 極値周りの処理の改善
- 低周波数及び高周波数側の近似・外挿処理の改善
特に極値周りの処理は計算上無限大が発生するためどのように回避するか様々な手法が提案されているようです。また、低周波と高周波側の外挿も興味ある周波数範囲に対してどれほど敏感なのかによっても近似の重要性が変わってきます。
例えば、1eV程度のバンド間遷移が興味の対象であるときには低エネルギー側の近似は重要ではないかもしれません。一方で、超伝導ギャップなどの低エネルギー現象では10meV程度(100cm^-1くらい)以下のエネルギー範囲が重要になります。低エネルギー側に着目する際は、予想以上に高エネルギー側の振る舞いが影響を与えることも有り、注意が必要です。
参考文献:A. Charnukha他、Superconductivity-induced optical anomaly in an iron arsenide
【脇道】
実装のための調査の過程で1つ気になるトピックがありました。
それが、PETER LICHV£Rらによる
です。
この論文では、同じ反射率データを入力に使用し、いくつかの商用ソフトウェアを使ってKK変換を実行すると、異なる結果が得られるという問題を指摘しています。
 |
| 商用ソフトウェアごとの計算結果。絶対値だけでなく周波数依存性も異なる |
闇が深い。
この論文ではその原因までは明らかにしていませんが、同様の問題が、異なる研究グループの論文の間でも生じている可能性があります。つまり研究者ごとに使用している変換プログラムが異なることで、異なる研究グループ間のデータに解析由来の誤差が生じているということです。
この様な問題は、測定結果の解析一般、また理論計算においても生じうる問題です。対策としては、コミュニティの中で標準的な処理結果を定め、その結果を再現できることを一つの基準とすることが挙げられます。また同じ研究グループ内での測定・計算結果だとしても、実行者依存性、装置の経年変化、計算ライブラリのバージョンの変化などの影響が考えられるため、以前測定したサンプルを測定し直すなどのレファレンス測定の重要性は変わりません。
オリジナリティの高い測定・計算を行う場合ほど、注意が必要な観点といえます。
閑話休題、問題点が残るとはいえ、たたき台としての初版のコードが簡単に作成できるのは助かります。一方で、さらなる改善には専門的な知識、つまり何が正しいか、どうあるべきかという判断軸を使用者が持っていることが必要だと感じました。
【まとめ】
今回は光学伝導度のKK変換についてAI、具体的にはClaudeを使って実装することに取り組んでみました。AIはやりたいことを入力すればいとも簡単にコードを出力してくれ、研究や作業の助けとなることがわかります。入力はテキストだけではなく、画像やPDF丸ごとでも対応でき、その解析力の高さに脱帽です。
この様な技術により、実験研究者が理論との比較を行うことが容易になったり、理論計算の中身をパラメータを変えながら手元で再現することでその理論の理解を深めるために利用できると考えられます。
今後ますますAIの能力は高まり、出力結果は改善されていくでしょう。一方で、AIは結果の正しさ、妥当性までは保証してくれませんし、使用した結果の責任もとってはくれません。AIを正しく活用するには、その出力を適切に判断できるよう、使用者の能力の向上も合わせて大切になることが実感できた今回の取組でした。
それでは、聖しクリスマス!KK!
【その他参考文献】
- Wikipedia「クラマース・クローニッヒの関係式
- 田島節子、高温超伝導体の電荷応答」
- H.イバッハ、H.リュート、固体物理学 改訂新版
- Esposito, R. J.他、A COMPUTER PROGRAM FOR A KRAMERS-KRONIG TRANSFORMATION OF THE OPTICAL REFLECTIVITY
- H Okamura、A simple method for the Kramers-Kronig analysis of reflectance spectra measured with diamond anvil cell
- Patrick D Fitzgerald、Numerical Approximation of Kramers-Kronig Relations to Transform Discretized Absorption Data
- Jérôme Lucas; Emmanuel Géron; Thierry Ditchi; Stéphane Holé、A fast Fourier transform implementation of the Kramers- Kronig relations: Application to anomalous and left handed propagation
- Robert Nitsche and Torsten Fritz、Determination of model-free Kramers-Kronig consistent optical constants of thin absorbing films from just one spectral measurement: Application to organic semiconductors
- D. M. Bastidas他、Application of Kramers-Kronig relationships for titanium impedance data validation in a Ringer's solution
- S. S. Ng他、KRAMERS-KRONIG ANALYSIS OF INFRARED REFLECTANCE SPECTRA WITH A SINGLE RESONANCE
- Kiyoshi Yamamoto, Akio Masui, and Hatsuo Ishida、Kramers–Kronig analysis of infrared reflection spectra with perpendicular polarization
- Julien Levallois他、Magneto-optical Kramers-Kronig analysis
- A.B.Kuzmenko、Kramers-Kronig constrained variational analysis of optical spectra
【実際に使用したコード】
In [1]:
!pip install nbconvert
In [ ]:
from google.colab import drive
drive.mount('/content/drive')
In [ ]:
!jupyter nbconvert --to html /content/drive/MyDrive/Colab Notebooks/optical_KK変換.ipynb
In [ ]:
import matplotlib.pyplot as plt
import numpy as np
In [ ]:
def lorentz_model(w, w_TO, w_LO, epsilon_inf, gamma):
# Sを計算
S = epsilon_inf * ((w_LO**2 / w_TO**2) - 1)
# 複素誘電関数を計算
epsilon = epsilon_inf + (S * w_TO**2) / (w_TO**2 - w**2 - 1j*w*gamma)
return epsilon
def calculate_reflectivity(epsilon):
# 複素屈折率を計算
n_tilde = np.sqrt(epsilon)
# 反射率を計算
R = np.abs((n_tilde - 1) / (n_tilde + 1))**2
return R
# パラメータの設定
w_TO = 100 # 横波光学フォノン周波数
w_LO = 120 # 縦波光学フォノン周波数
epsilon_inf = 3.0 # 高周波誘電定数
gamma = 5 # フォノン減衰定数
# 周波数範囲の設定
w = np.linspace(50, 150, 1000)
# 複素誘電関数の計算
epsilon = lorentz_model(w, w_TO, w_LO, epsilon_inf, gamma)
# 反射率の計算
R = calculate_reflectivity(epsilon)
# プロット
plt.figure(figsize=(10, 6))
plt.plot(w, R)
plt.xlabel('Frequency (cm$^{-1}$)')
plt.ylabel('Reflectivity')
plt.title('Simulated IR Reflectivity Spectrum')
plt.grid(True)
plt.show()
In [ ]:
# ローレンツモデルによる光学反射率と光学伝導度の計算
def lorentz_model(w, w_TO, w_LO, epsilon_inf, gamma):
S = epsilon_inf * ((w_LO**2 / w_TO**2) - 1)
epsilon = epsilon_inf + (S * w_TO**2) / (w_TO**2 - w**2 - 1j*w*gamma)
return epsilon
def calculate_reflectivity(epsilon):
n_tilde = np.sqrt(epsilon)
R = np.abs((n_tilde - 1) / (n_tilde + 1))**2
return R
def calculate_optical_conductivity(w, epsilon, epsilon_inf):
# 光学伝導度の計算
sigma = -1j * w * (epsilon - epsilon_inf) / (4 * np.pi)
return sigma
# パラメータの設定
w_TO = 100 # 横波光学フォノン周波数 (cm^-1)
w_LO = 120 # 縦波光学フォノン周波数 (cm^-1)
epsilon_inf = 3.0 # 高周波誘電定数
gamma = 100 # フォノン減衰定数 (cm^-1)
# 周波数範囲の設定 (cm^-1 から rad/s に変換)
w_cm = np.linspace(1, 10000, 10000)
w = w_cm * 2 * np.pi * 3e10 # cm^-1 から rad/s に変換
# 複素誘電関数の計算
epsilon = lorentz_model(w_cm, w_TO, w_LO, epsilon_inf, gamma)
# 反射率の計算
R = calculate_reflectivity(epsilon)
# 光学伝導度の計算
sigma = calculate_optical_conductivity(w, epsilon, epsilon_inf)
# プロット
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(10, 15))
# 反射率のプロット
ax1.plot(w_cm, R)
ax1.set_xlabel('Frequency (cm$^{-1}$)')
ax1.set_ylabel('Reflectivity')
ax1.set_title('Simulated IR Reflectivity Spectrum')
ax1.grid(True)
# 光学伝導度の実部のプロット
ax2.plot(w_cm, sigma.real)
ax2.set_xlabel('Frequency (cm$^{-1}$)')
ax2.set_ylabel('Re[σ(ω)] (s$^{-1}$)')
ax2.set_title('Real Part of Optical Conductivity')
ax2.grid(True)
# 光学伝導度の虚部のプロット
ax3.plot(w_cm, sigma.imag)
ax3.set_xlabel('Frequency (cm$^{-1}$)')
ax3.set_ylabel('Im[σ(ω)] (s$^{-1}$)')
ax3.set_title('Imaginary Part of Optical Conductivity')
ax3.grid(True)
plt.tight_layout()
plt.show()
In [ ]:
#クラマース・クローニッヒ変換の実装
import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt
#クラマース・クローニッヒ変換
def kk_transform(w, R):
def integrand(w_prime, w):
return (np.log(R(w_prime)) - np.log(R(w))) / (w_prime**2 - w**2)
phi = np.zeros_like(w)
for i, wi in enumerate(w):
phi[i] = -(wi / np.pi) * integrate.quad(integrand, w[0], w[-1], args=(wi,))[0]
return phi
#複素屈折率の計算
def calculate_n_k(w, R, phi):
sqrt_R = np.sqrt(R)
n = (1 - R) / (1 + R - 2 * sqrt_R * np.cos(phi))
k = (2 * sqrt_R * np.sin(phi)) / (1 + R - 2 * sqrt_R * np.cos(phi))
return n, k
#複素誘電率の計算
def calculate_epsilon(n, k):
epsilon_real = n**2 - k**2
epsilon_imag = 2 * n * k
return epsilon_real, epsilon_imag
#光学伝導度の計算
def calculate_optical_conductivity(w, epsilon_imag):
# 光速 (cm/s)
c = 2.99792458e10
# 真空の誘電率 (F/cm)
epsilon_0 = 8.854187817e-14
# 角周波数 (rad/s)
omega = 2 * np.pi * c * w
# 光学伝導度 (Ω^-1 cm^-1)
# sigma = omega * epsilon_0 * epsilon_imag / (4 * np.pi)
sigma = w * epsilon_imag / (4 * np.pi)
return sigma
# 上のセルで求めた結果を流用
w = w
R = R
# KK変換
phi = kk_transform(w, lambda x: np.interp(x, w, R))
# 複素屈折率の計算
n, k = calculate_n_k(w, R, phi)
# 複素誘電率の計算
epsilon_real, epsilon_imag = calculate_epsilon(n, k)
# 光学伝導度の計算
sigma_kk = calculate_optical_conductivity(w, epsilon_imag)
# 結果のプロット
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(15, 15))
ax1.plot(w, R)
ax1.set_xlabel('Wavenumber (cm$^{-1}$)')
ax1.set_ylabel('Reflectance')
ax1.set_title('Measured Reflectance')
ax2.plot(w, epsilon_real, label='Real part')
ax2.plot(w, epsilon_imag, label='Imaginary part')
ax2.set_xlabel('Wavenumber (cm$^{-1}$)')
ax2.set_ylabel('Dielectric Function')
ax2.set_title('Complex Dielectric Function')
ax2.legend()
ax3.plot(w, n, label='n')
ax3.plot(w, k, label='k')
ax3.set_xlabel('Wavenumber (cm$^{-1}$)')
ax3.set_ylabel('Refractive Index')
ax3.set_title('Complex Refractive Index')
ax3.legend()
ax4.plot(w, sigma_kk)
ax4.set_xlabel('Wavenumber (cm$^{-1}$)')
ax4.set_ylabel('Optical Conductivity (Ω$^{-1}$ cm$^{-1}$)')
ax4.set_title('Optical Conductivity')
plt.tight_layout()
plt.show()
In [ ]:
#理論式とKK変換した値の比較
import pandas as pd
# cm^-1 から rad/s に変換
w = w_cm * 2 * np.pi
w_cm = w / 2 / np.pi
# DataFrameの作成
df = pd.DataFrame({
'w': w,#波数
'Sigma': sigma,#誘電率から直接求めた光学伝導度
'Sigma_KK': sigma_kk#誘電率から求めた反射率をKK変換して求めた光学伝導度
})
# プロット
plt.figure(figsize=(10, 6))
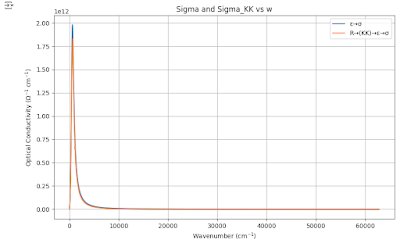
plt.plot(df['w'], df['Sigma'], label='ε→σ')
plt.plot(df['w'], df['Sigma_KK'], label='R→(KK)→ε→σ')
# グラフの設定
plt.xlabel('Wavenumber (cm$^{-1}$)')
plt.ylabel('Optical Conductivity (Ω$^{-1}$ cm$^{-1}$)')
plt.title('Sigma and Sigma_KK vs w')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()








コメント
コメントを投稿