「鉄系SCはs±波なの？s++波なの？」論争って最近どうなってるの？？

 【イントロ】

　超伝導現象は、超伝導転移温度(Tc)と呼ばれる相転移温度以下で急激にゼロになる現象です。その劇的な変化もさることながら、この超伝導現象をより高い温度で実現することができれば、電力伝達のロスを最小限にし省エネルギー化が実現できることから長年研究が続けられています。研究とともに銅酸化物やMgB2、コバルト酸化物、水素化物、そして鉄系超伝導体など、様々な超伝導物質が報告されています。

　鉄系超伝導体は、２００８年にLaFeAs(O,F)が東工大のKamihara先生たちにより報告[1]されて以来一大研究分野となり、１３年たった今も様々な話題を提供してくれています。マルチバンド超伝導[*]、スピン電荷ボルテックス秩序[*]、軌道選択的モット転移[*]、フント金属[*]、トポロジカル物性[*]、マヨラナ励起[*]、電子ネマティック相[*]・・・どれも追求しがいのあるテーマになっています。

　その話題の中に、「超伝導ギャップの位相は反転しているのか？」というものがあります。これは、電子的フェルミ面(電子面)とホール的フェルミ面(ホール面)をもつマルチバンドな鉄系超伝導体の場合、超伝導秩序パラメータである超伝導ギャップ、Δ = |Δ|exp(iθ)、の位相θが各フェルミ面間で符号反転しているのか？という問題です。様々な実験が行われ、「位相は反転しているよ」という「s±波説」(いわゆるスピンゆらぎ起源説)[2,3]と「いや位相は反転してないよ」という「s++波説」(いわゆる軌道ゆらぎ起源説)[4]の”””熱い”””議論がかわされました。

図、超伝導ギャップ対称性のありうる可能性[11]

　そこで本記事では、この論争について、最近の結果も踏まえて、個人的に興味のある以下の5つの現象観点からまとめてみました。

• 不純物効果
• 準粒子干渉
• 超伝導ギャップノード構造
• ジョセフソン接合ほか
• 中性子散乱の共鳴ピーク

なお、議論の内容はおもに文献[5,6,7]等を参考にしています。特にNatureに掲載されたFernandesらのレビュー[5]は最新の研究状況がわかるのでオススメです。

【論争】

　鉄系超伝導体には、1111系(LaFeAs(O,F)など)、122系(BaFe2(As,P)2など)、111系(LiFeAsなど）、11系(FeSeなど）他様々な物質系があります。その中には①ホール面と電子面の両方を持つ物質の他に、②ホール面のみをもつもの(KFe2As2など)、③電子面のみをもつもの(KFe2Se2など)もあります。本記事では符号反転の議論がなされた①の物質系に注目します。

●不純物効果

　「超伝導体に非磁性不純物をいれてもTcは変わらない」、いわゆるアンダーソンの定理が通常のs波超伝導体の場合は成り立ちます[8]。鉄系超伝導の場合、伝導面にあるFeサイトを元素置換することで超伝導が発現(Ba(Fe,Co)2As2など)しますが、10%程度の置換に対してもTc~20K程度の高い転移温度が実現します。また、様々な元素(Mn, Ru, Co, Ni, Cu, Zn)を不純物置換した場合もTcは大きく減少しないことが報告されています[9]。これらの結果に基づきOnari先生たちは、

「符号反転を伴うs±波超伝導体(SC)の場合はTcが不純物に敏感に反応し、大きく減少する。そうなっていないならば、s++波SCが実現しているはず」

というs++波SC説を提唱しました[10]。

図、ギャップ対称性による不純物効果の違い[10]

　不純物効果はs++波SC説を支持する重要な結果でしたが、s±波SC説を支持する Hirschfeld先生たちによって、 

「不純物効果って、元素置換したらキャリア数も変わるし何みてるかわからんくない？ あと、Tcの減少率って不純物ポテンシャルの形状とか、バンド間/バンド内散乱の比率、 ギャップ形状にも依存するから減少率ってそんな高くないのでは？むしろ、純粋な状態ではs±波SC状態が実現していて、不純物が増えるとs++波SCになるのでは？」 

という理論を提唱しました[11]。

　キャリア数を変えず不純物量を変える手段として、電子線照射、陽子線照射法があります。電子、陽子を結晶にぶつけて、結晶内の原子を弾き飛ばすことで欠陥を生成し不純物となす手法となっています。Prozorov先生たちはこの手法をBa(Fe,Ru)2As2に適用し、s±波SC説に一致するTc減少率を観測することに成功しています[12]。また、陽子線照射をBa(Fe,Rh)2As2に適用することで、不純物量の増加とともにTcの減少が飽和する、まさにs±波SC→s++波SC変化説を支持する結果を得ることに成功しています[13]。

図、陽子線照射によるギャップ対称性の変化[13]

　以上のことから、当初はs++波SC説を強く支持する不純物効果でしたが、理論と実験の発展により、必ずしもs±波SCで説明できないわけではない状況になっている印象です。

●準粒子干渉

　一般に、超伝導ギャップの位相情報を得ることは困難です。数少ない位相情報を取得する手法が走査型トンネル分光による磁場下における準粒子干渉法です。これは磁場中で波数空間の情報を取得できる走査型トンネル分光法の利点を活用し、磁場による準粒子の符号反転散乱と符号保存散乱の干渉強度変化が異なることを利用して、符号反転の有無を明らかにする手法です[14]。

　Hanaguri先生たちは銅酸化物SC研究で発展したこの磁場中準粒子干渉法を、清浄表面が得られるFe(Se,Te)に適用し、s±波SCを支持する結果をScience誌に報告しました[15]。この結果は、s±波SCを強く支持ものなっていましたが、Yamakawa先生たちは、鉄系超伝導の場合、s++波SCでも準粒子干渉法の結果を説明できる理論を提案しました[16]。このことから、準粒子干渉法の結果だけでは(何事もそうですが)、必ずしもs±波SCとs++波SCを区別できない状況になっているようです(ほんまか？)。単一バンドのシンプルな銅酸化物と比較してマルチバンドな鉄系SCはそれだけ現象の解析が大変なんですね。

図、ギャップ対称性の違いによる磁場による準粒子干渉の変化。
カラースケールが1桁違うのはご愛嬌。[16]

　一方で、その後も走査型トンネル分光を用いた研究は進展し、軌道選択的クーパー対形成や反強磁性スピンゆらぎの兆候などs±波SCを支持する準粒子干渉の結果がFeSe、LiFeAs、Ba(Fe,Co)2As2で報告されています[17,18,19]。

図、FeSeのs±波SC説と一致する、軌道選択クーパー対形成[17]

●超伝導ギャップノード構造

　超伝導対称性を決める手段の1つが、波数空間での超伝導ギャップ構造を決定することです。例えば、銅酸化物SCでは、特定の波数空間方向にギャップがゼロになるノードが存在することがd波SCの証拠の1つとなっています。鉄系超伝導の場合、d波SCのように対称性から要請されるノードは基本的に存在していません。しかしs±波SCとs++波SCのどっちの寄与が優勢かでノードが偶発的に現れる波数空間位置が異なることから、その位置を特定しようという取り組みが行われました。

［注；KFe2As2がd波SCという議論が別にあります(※１、※２)］

　多くの鉄系SC物質がノードのないフルギャップ構造を示す中、ノード構造の研究が行われたのがBaFe2(As,P)2です。この物質は、磁場侵入長、熱伝導度、比熱、NMR測定からノードの存在が示唆されています[20,21,22]。そこでノードの波数空間位置を特定するため、角度分解熱伝導度測定とARPESが行われました。

　日本グループによる角度分解熱伝導度測定[23]とARPES[24]では電子面にループ状のノードが存在することが報告されており、これはs++波SCの寄与があることを示唆[25]しています。一方で、中国グループによるARPES[26]ではホール面のZ点付近に水平ノードが存在することが報告されており、s±波SCに基づく理論[27]と整合しています。この不一致の原因は明らかになっていませんが、ノードの位置は不純物濃度次第で変化すると理論的に提案されています[25]。実際、日本グループと中国グループの測定で使用されたサンプルの作成方法がそれぞれ異なるため、不純物濃度が異なっていた可能性はあります。

【注；多結晶を用いた中性子散乱でも水平ノードの可能性が指摘されています[＊]]

図、中国グループによるBaFe2(As,P)2のノード構造の観測[26]

　また、そもそも「ノードが偶発的に生じたものなのか」という点を検証するため、電子線照射で不純物濃度をコントロールしたサンプルで磁場侵入長の測定が行われました。その結果、不純物濃度の増加とともにノードが消えフルギャップ構造が現れる、s±波SCに一致する振る舞いが報告されています[28]。

図、不純物濃度によるギャップ構造の変化[28]

　以上の結果から、ノードのある鉄系SCについて、その波数空間上の位置ははっきり決着がついていない印象です。一方で、ノードの位置、ノードの有無がサンプルごと(不純物濃度ごと）に異なること、ノードが対称性に守られたものではなく偶発的なものであること、また、不純物濃度によってs±波SCかs++波SCの両方が実現している可能性は高そうです。

●ジョセフソン接合ほか

　超伝導ギャップの位相を直接検証しs±波SCを支持する結果と考えられていたのが、2010年に報告された、Nd1111の走査型SQUID測定による半整数磁気フラックス量子相転移の検出[29]です。この研究は銅酸化物のd波超伝導の位相検出にも成功したIBMグループにより巧妙に実験がデザインされていましたが、多結晶による結果であったこともあり、さらに別の位相敏感な測定が求められていました。

　その後、Nb/(Ba,K)Fe2As2またはNb/(Ba,Na)Fe2As2を用いたジョセフソン接合の研究が報告[30,31]され、d波SCとs++波SCの可能性を強く排除し、s±波SC説をほぼ完全に支持する結果が報告されています。ただ、この結果もs++波SCに基づいて技巧を尽くせば説明できる可能性は排除できないかもしれません。

　また、Fe(Se,Te)がs±波SCの場合、高次トポロジカル超伝導状態となることが理論的に予想され、実際に対応するヘリカルヒンジゼロモードが検出されたこともs±波SC説を支持する結果となっています[32]。マヨラナ励起の存在の有無から、間接的にギャップ対称性を決めることができそうですが、マヨラナ励起の観測自体が大変な研究になりそうです。

図、Fe(Se,Te)が高次トポロジカル超伝導体になる可能性の概念図[32]

　

●中性子散乱の共鳴ピーク

　もしs±波SC説が正しいならば、超伝導転移温度以下で動的磁気感受率がコヒーレンス因子により増強され、特定の波数ベクトルに共鳴ピークが観測されることが期待されます。実際、QiuやChristiansonによる非弾性中性子散乱実験でそのような共鳴ピークが観測されており、観測された波数ベクトルがホール面と電子面間のネスティングベクトルと対応することから、反強磁性スピンゆらぎに由来するs±波SC説を支持する結果として解釈されています[33,34]。

 

図、Fe(Se,Te)の共鳴ピークの温度、エネルギー依存性[33]

　一方で、Onari先生たちは有効5バンドモデルとRPA近似を用いた計算から、観測された共鳴ピークはブロードでありs++波SC説に基づいても実験を説明できることを指摘しています[35]。

　Onari先生達の理論提案後もいくつかの実験が報告されています。Hongらは二次元性の高いKCa2Fe4As4F2ではOnari先生たちが指摘するように共鳴ピークがギャップサイズを超えるエネルギー領域まで広がっておりs±波SC説の解釈では難しいことを報告しています[36]。一方で、ZhangらはNa(Fe,Cu)Asの共鳴ピーク位置の温度依存性を測定することで、s±波SC説でなければ説明できないことを主張しています[37]。また、XieらはCaKFe4As4の測定から、多軌道性を反映し、複数の波数ベクトルごとに、共鳴ピークと対応するギャップサイズが存在し、それぞれがs±波SC説の枠内で説明できることを主張しています[38]。

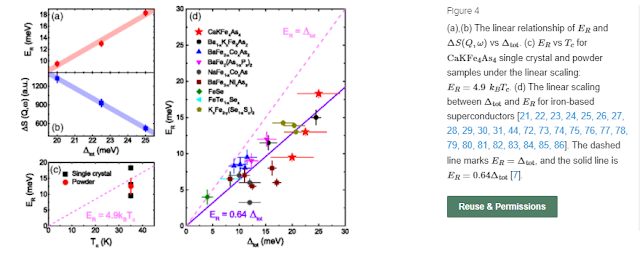図、複数ギャップと複数共鳴ピークのエネルギーの関係[38]

　以上の結果から、中性子散乱の共鳴ピークの存在はs±波SC説の証拠と当初は考えられましたが、s++波SC説でも解釈できることが主張され、決定的な実験とはなっていないようです。やはり、多軌道性に伴う複数ギャップ、複数反強磁性スピンゆらぎの存在が議論を複雑にしている印象です。

【まとめ】

　鉄系SCの超伝導ギャップ対称性の符号反転の有無論争について、興味がある測定手段の近況を調べてみました。クリーンな状態ではs±波SCが実現している印象を受けましたが、どの実験手段でも決定的な実験結果といえるものは未だに得られていないようです。多バンド系での位相の決定って難しいですね。

　一方で、不純物濃度で対称性、ギャップ構造が大きく変わることが明らかになっています。様々な物質系存在する鉄系SCでは、s±波SCとs++波SCのどちらかが実現しているというよりも、サンプルや組成次第で、両方が実現、競合しているのが真実に近いのかもしれません。個人的にはクリーンなサンプルでどっちが実現しているのかはっきりすると良いなと思っていますが、決定的な測定手段、最高のサンプルが今後現れることを祈って、この分野の進展を楽しみにしたいと思います。

【参考文献】

[1]. Y. Kamihara et al., J. Am. Chem. Soc. 2008, 130, 11, 3296–3297

[2]. I. I. Mazin et al., Phys. Rev. Lett. 101, 057003 – Published 29 July 2008,

 K. Kuroki et al., Phys. Rev. Lett. 101, 087004 – Published 22 August 2008

[3]. Y. Nomura et al., Phys. Rev. Lett. 112, 027002 – Published 15 January 2014

[4]. H. Kontani et al., Phys. Rev. Lett. 104, 157001 – Published 15 April 2010

[5]. Fernandes, R.M., Coldea, A.I., Ding, H. et al. Iron pnictides and chalcogenides: a new paradigm for superconductivity. Nature 601, 35–44 (2022).

[6]. 芝内 孝禎, 松田 祐司, 鉄系高温超伝導体の超伝導対称性と電子状態相図 （解説）, 日本物理学会誌/68 巻 (2013) 9 号, 

紺谷 浩, 非従来型超伝導体の理論：鉄系超伝導体を中心に（第64回物性若手夏の学校　集中ゼミ2）, 物性研究, Vol. 8 No. 1 （2020年2月号）

[7]. 永井佑紀, 鉄系超伝導体の超伝導対称性に関する理論的研究

[8]. Anderson, P. W. (1959). "Theory of dirty superconductors". J. Phys. Chem. Solids.

[9]. J. Li et al., Phys. Rev. B 85, 214509 – Published 11 June 2012

[10]. Seiichiro Onari and Hiroshi Kontani, Phys. Rev. Lett. 103, 177001 – Published 21 October 2009

[11]. D. V. Efremov et al., Phys. Rev. B 84, 180512(R) – Published 16 November 2011, 

P J Hirschfeld et al 2011 Rep. Prog. Phys. 74 124508

[12]. R. Prozorov et al., Phys. Rev. X 4, 041032 – Published 18 November 2014

[13]. G. Ghigo et al., Phys. Rev. Lett. 121, 107001 – Published 4 September 2018

[14]. 花栗 哲郎, 超伝導体を探る針～分光イメージング走査型トンネル顕微鏡～ （解説）, 日本物理学会誌/66 巻 (2011) 3 号

[15]. T. HANAGURI et al., SCIENCE 7, Jul 2017,  Vol 357, Issue 6346,  pp. 75-80

[16]. Youichi Yamakawa and Hiroshi Kontani, Phys. Rev. B 92, 045124 – Published 27 July 2015

[17]. P. O. SPRAU et al., SCIENCE, 7 Jul 2017, Vol 357, Issue 6346, pp. 75-80

[18]. Allan, M., Lee, K., Rost, A. et al. Identifying the 'fingerprint' of antiferromagnetic spin fluctuations in iron pnictide superconductors. Nature Phys 11, 177–182 (2015).

[19]. M. L. Teague st al., Phys. Rev. Lett. 106, 087004 – Published 24 February 2011

[20]. K. Hashimoto et al., Phys. Rev. B 81, 220501(R) – Published 1 June 2010

[21]. J. S. Kim et al., Phys. Rev. B 81, 214507 – Published 4 June 2010

[22]. Yusuke Nakai et al., Phys. Rev. B 81, 020503(R) – Published 6 January 2010

[23]. M. Yamashita et al., Phys. Rev. B 84, 060507(R) – Published 18 August 2011

[24]. Yoshida, T., Ideta, S., Shimojima, T. et al. Anisotropy of the superconducting gap in the iron-based superconductor BaFe2(As1-xPx)2. Sci Rep 4, 7292 (2014).

[25]. Tetsuro Saito et al., Phys. Rev. B 88, 045115 – Published 11 July 2013

[26]. Zhang, Y., Ye, Z., Ge, Q. et al. Nodal superconducting-gap structure in ferropnictide superconductor BaFe2(As0.7P0.3)2. Nature Phys 8, 371–375 (2012).

[27]. Katsuhiro Suzuki et al., J. Phys. Soc. Jpn. 80, 013710 (2011)

[28]. Mizukami, Y., Konczykowski, M., Kawamoto, Y. et al. Disorder-induced topological change of the superconducting gap structure in iron pnictides. Nat Commun 5, 5657 (2014).

[29]. Chen, CT., Tsuei, C., Ketchen, M. et al. Integer and half-integer flux-quantum transitions in a niobium–iron pnictide loop. Nature Phys 6, 260–264 (2010).

[30]. A. A. Kalenyuk et al., Phys. Rev. Lett. 120, 067001 – Published 6 February 2018

[31]. A. V. Burmistrova et al., Phys. Rev. B 91, 214501 – Published 2 June 2015

[32]. Mason J. Gray et al., Nano Lett. 2019, 19, 8, 4890–4896

[33]. Yiming Qiu et al., Phys. Rev. Lett. 103, 067008 – Published 7 August 2009

[34]. Christianson, A., Goremychkin, E., Osborn, R. et al. Unconventional superconductivity in Ba0.6K0.4Fe2As2 from inelastic neutron scattering. Nature 456, 930–932 (2008).

[35]. Seiichiro Onari and Hiroshi Kontani, Phys. Rev. B 84, 144518 – Published 24 October 2011

[36]. Wenshan Hong et al., Phys. Rev. Lett. 125, 117002 – Published 10 September 2020

[37]. Chenglin Zhang et al., Phys. Rev. B 88, 064504 – Published 9 August 2013

[38]. Tao Xie et al., Phys. Rev. Lett. 120, 267003 – Published 29 June 2018